Příklady dobré praxe on-line výuky na ZČU – 10. díl (GeoGebra)

Světlana Tomiczková, Zlata Hokrová

V dnešním článku si ukážeme, že i geometrii lze skvěle učit on-line. Řeč bude o nástroji, který spojuje geometrii, algebru, tabulky, znázornění grafů, statistiku a infinitezimální počet a zároveň ho lze použít na všech úrovních vzdělávání – od základní školy až po vysokou. Seznamte se s aplikací GeoGebra.

O své zkušenosti s využitím této aplikace ve výuce se s námi podělí RNDr. Světlana Tomiczková, Ph.D., z Katedry matematiky Fakulty aplikovaných věd Západočeské univerzity v Plzni.

Co vás vedlo k zařazení aplikace GeoGebra do výuky a jak s ní pracujete?

Světlana Tomiczková: Učím geometrii pro studenty různých fakult na ZČU (FST, FAV, FPE), přičemž součástí kurikula jednotlivých předmětů jsou zobrazovací metody. Učíme tedy studenty, jak zobrazovat 3D prostor do roviny. Podle zaměření studentů se zabýváme jak různými typy rovnoběžného promítání (Mongeovo promítání, axonometrie, kótované promítání), tak promítáním středovým včetně lineární perspektivy. V dalších předmětech se pak věnujeme zobrazování křivek a ploch a konstrukcím na nich.

Protože je v obou případech dobré zprostředkovat studentům prostorovou vizualizaci problému a naučit je postupy konstrukcí, rozhodla jsem se k tomu využít nějaký dostupný program.

Pro 3D vizualizaci by bylo samozřejmě možné použít řadu profesionálních programů, které jsou buď zaměřené na matematiku (např. Mathematica nebo Maple), nebo je používají odborníci z různých oborů (AutoCAD, CATIA). Využívání těchto programů při výuce geometrie však naráží jednak na specifika těchto programů (jsou příliš komplikované a primárně určené k jiným účelům), jednak na poměrně vysoké náklady na pořízení licence pro výuku základních předmětů, které má absolvovat větší množství studentů.

Existují ovšem i volně dostupné nebo cenově přiměřené programy. Některé školy využívají pro 3D objekty software Sketchpad a pro 2D geometrii Cabri anebo právě GeoGebru, kterou jsem si pro výuku zvolila i já.

GeoGebra je interaktivní počítačový program určený pro geometrii, algebru i analýzu. Já využívám GeoGebru zejména při výuce geometrie, ale také v matematice při výuce funkcí.

Takto vypadá základní prostředí GeoGebry:

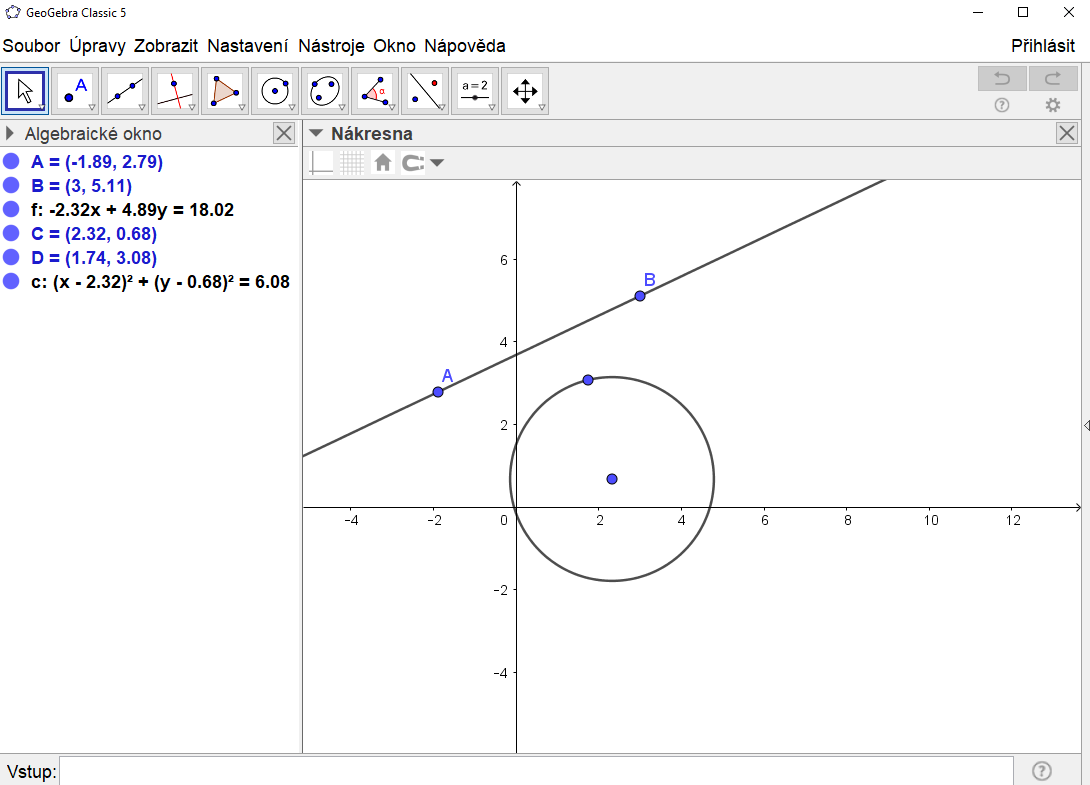
Kromě menu v horní části, zde vidíme dvě okna (toto základní nastavení lze podle potřeby a zkušeností rozšířit). V levém okně (Algebraické okno) je matematický zápis (rovnice, souřadnice, parametrické vyjádření) zobrazených objektů, v pravém okně (Nákresna) jsou pak objekty zobrazeny. GeoGebra je dynamický software, kde jsou obě okna propojena, což znamená, že pokud cokoliv změním v Nákresně (posunu bod, změním poloměr kružnice apod.), změní se také zápis v Algebraickém okně a obráceně. Objekty mohu zadávat buď přímo pomocí nástrojů na horní liště v Nákresně, nebo pomocí matematických zápisů v dolní části v okně Vstup.

Byla by ovšem škoda používat GeoGebru pouze jako nákresnu. Vzhledem k tomu, že je zde možné měnit zadání nebo jeho část a dívat se, jak se mění výsledek, lze GeoGebru využívat k názorným ukázkám nebo přímo pro práci žáků či studentů. Dále je možné celý postup krokovat, tedy zopakovat vznik výsledného objektu krok po kroku, díky čemuž má GeoGebra potenciál přinést do výuky nový rozměr. Jako ukázku můžeme uvést následující obrázky z výuky rovinné geometrie a matematiky:

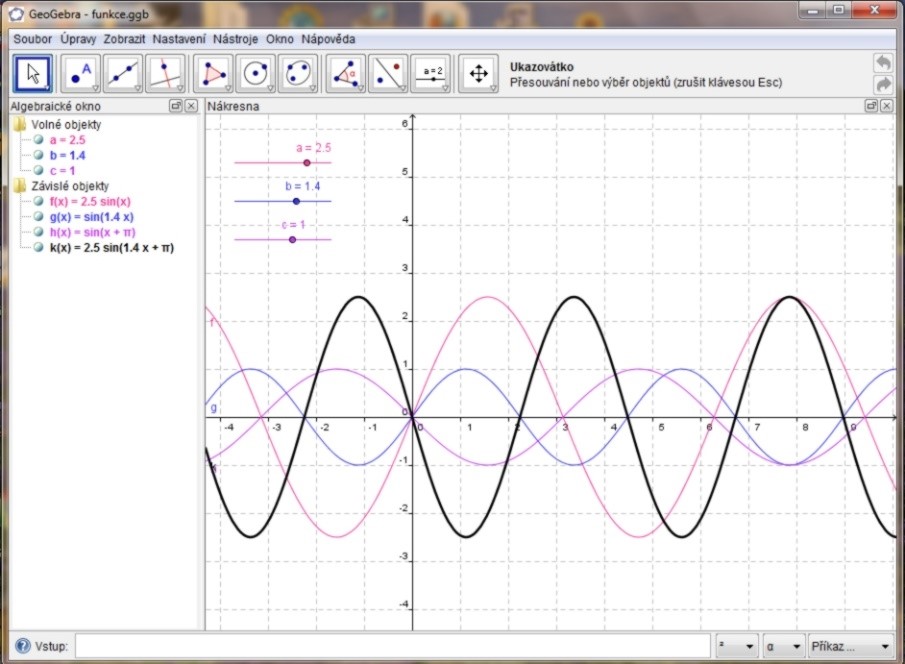
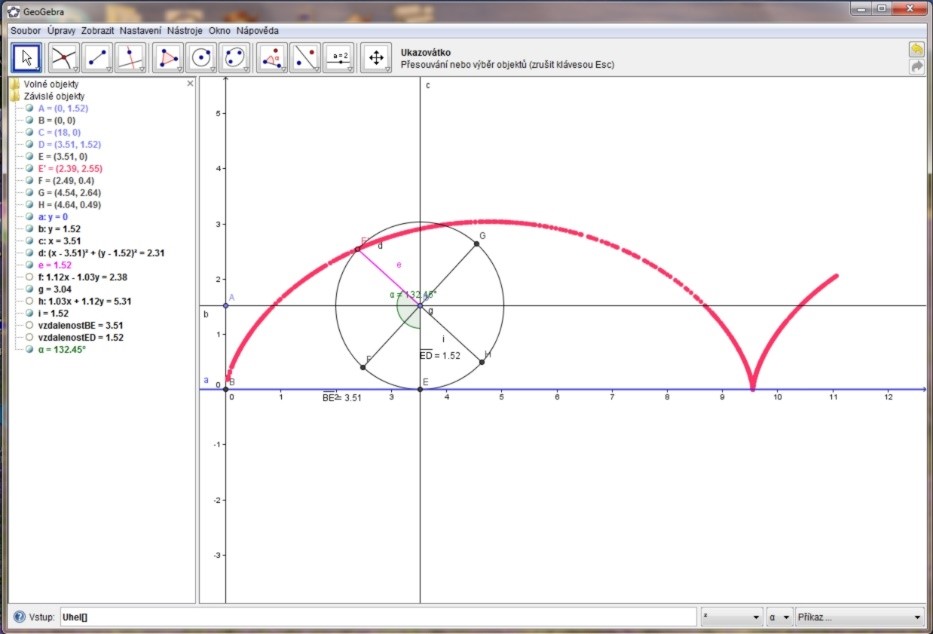
Další možností, kterou GeoGebra skýtá, je otevřít okno se zápisem konstrukce nebo okno s tabulkou.

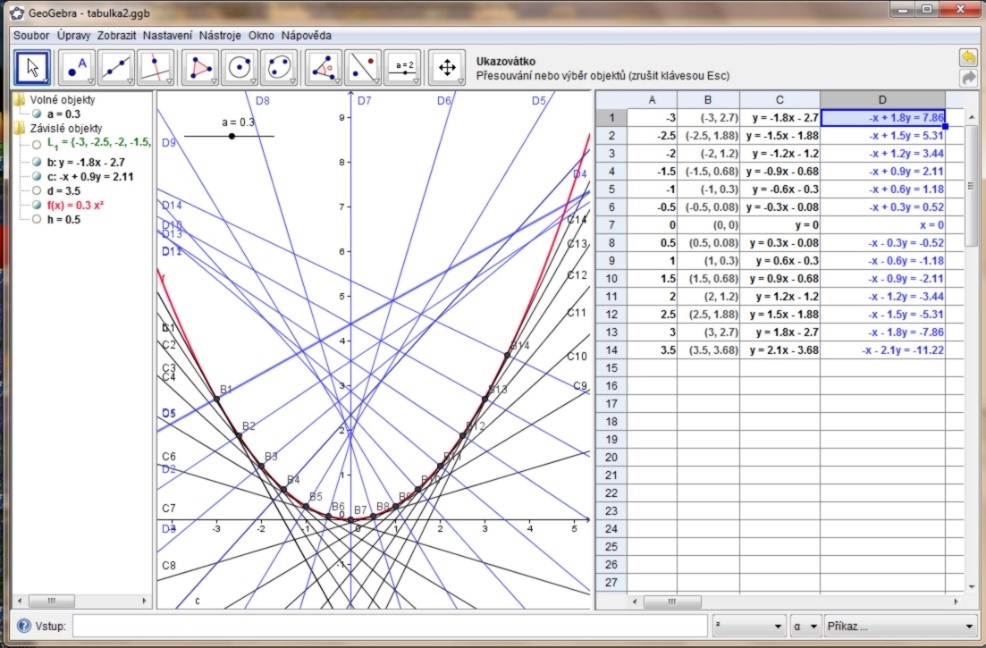
Během vývoje GeoGebry se postupně začala rozvíjet i 3D GeoGebra, která umí zobrazit trojrozměrné objekty, a tak mohly vzniknout materiály v GeoGebře propojující jak dynamickou složku úlohy, tak prostorovou vizualizaci.

Příklad: Rotační plocha je dána osou o a meridiánem m. Sestrojíme řez rotační plochy rovinou ρ, která je určena stopami. Takto vypadá úloha v GeoGebře (úloha je k dispozici zde):

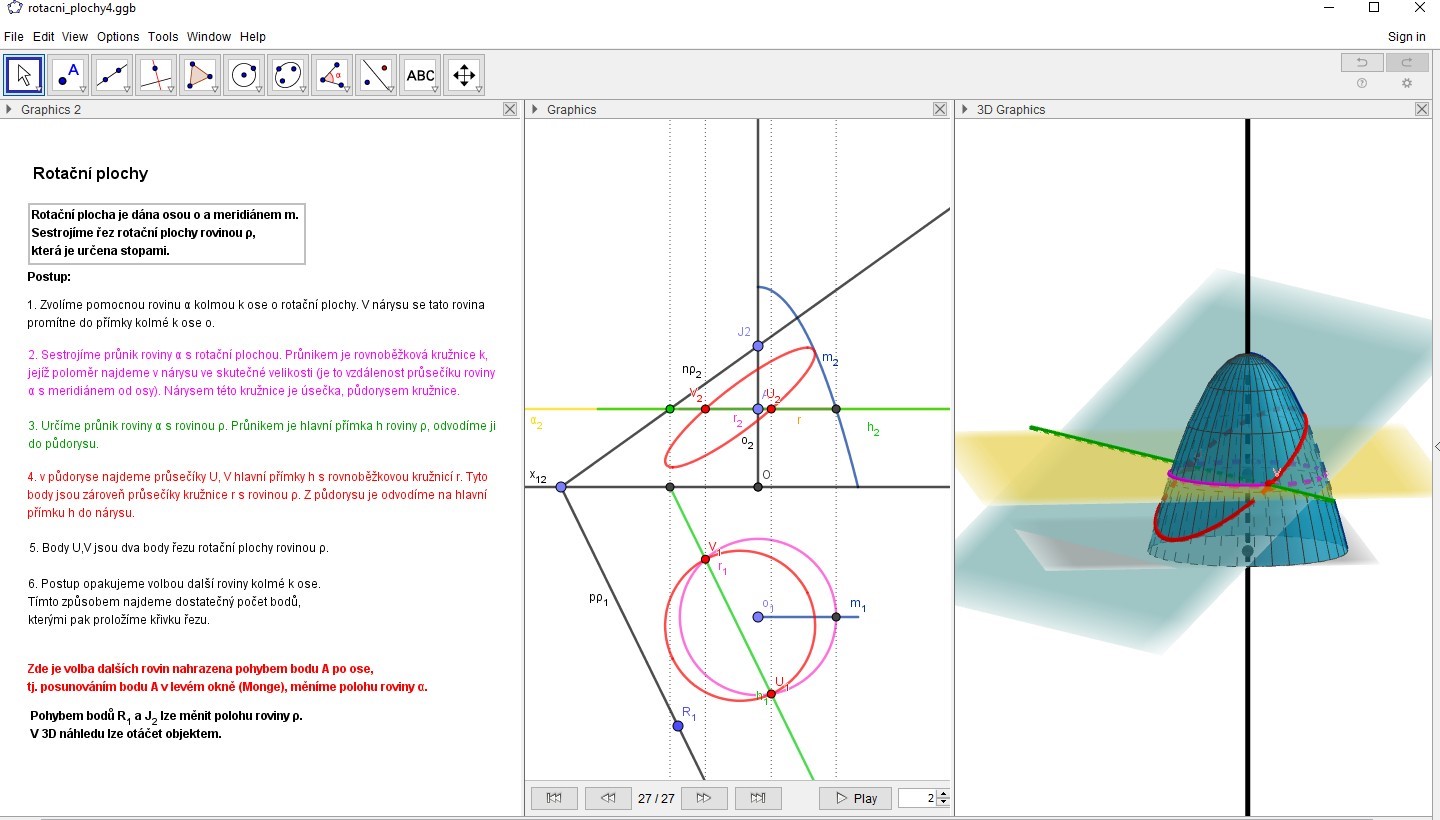
Zde je volba dalších pomocných rovin nahrazena pohybem bodu A po ose o, tj. posunováním bodu A v levém okně (Monge), měníme polohu pomocné roviny α. Dále lze pohybem bodů měnit polohu roviny ρ. V 3D náhledu lze otáčet celou scénou.

Příklad: Šroubová plocha je dána osou o, tvořící křivkou k a pravotočivou orientací. Sestrojíme řez šroubové plochy polorovinou α, procházející osou o. Na obrázku níže vidíme screenshot úlohy (úloha je k dispozici zde ):

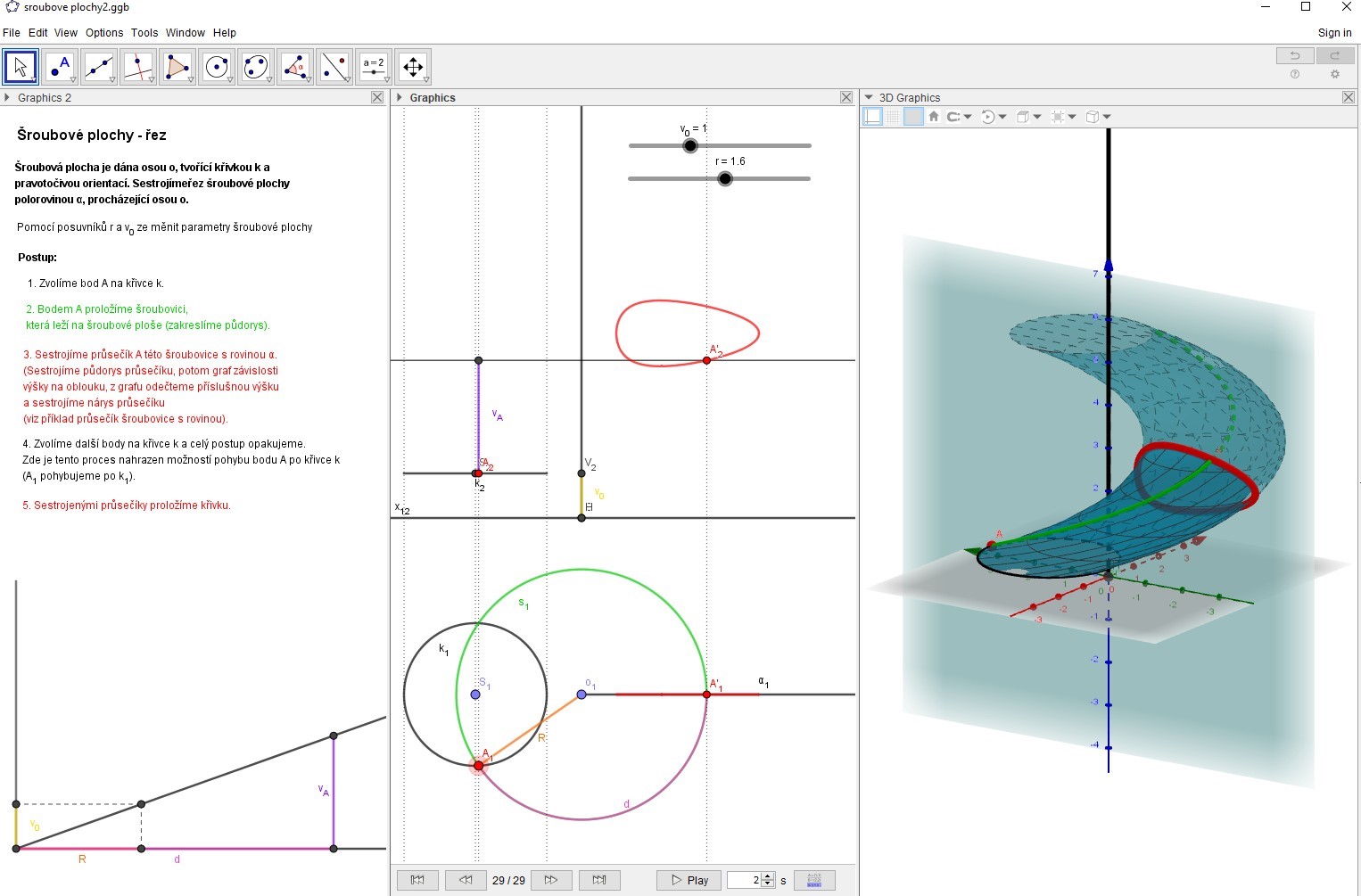
V úloze lze měnit pomocí posuvníků některé další parametry, jako je redukovaná výška závitu v₀ a poloměr tvořící kružnice k. Se změnou parametrů se dynamicky mění jak zadání a řešení v Mongeově promítání (nákresna – 2D), tak v 3D nákresně.

Příklad: Tečná rovina šroubové plochy (viz úloha, která je k dispozici zde).

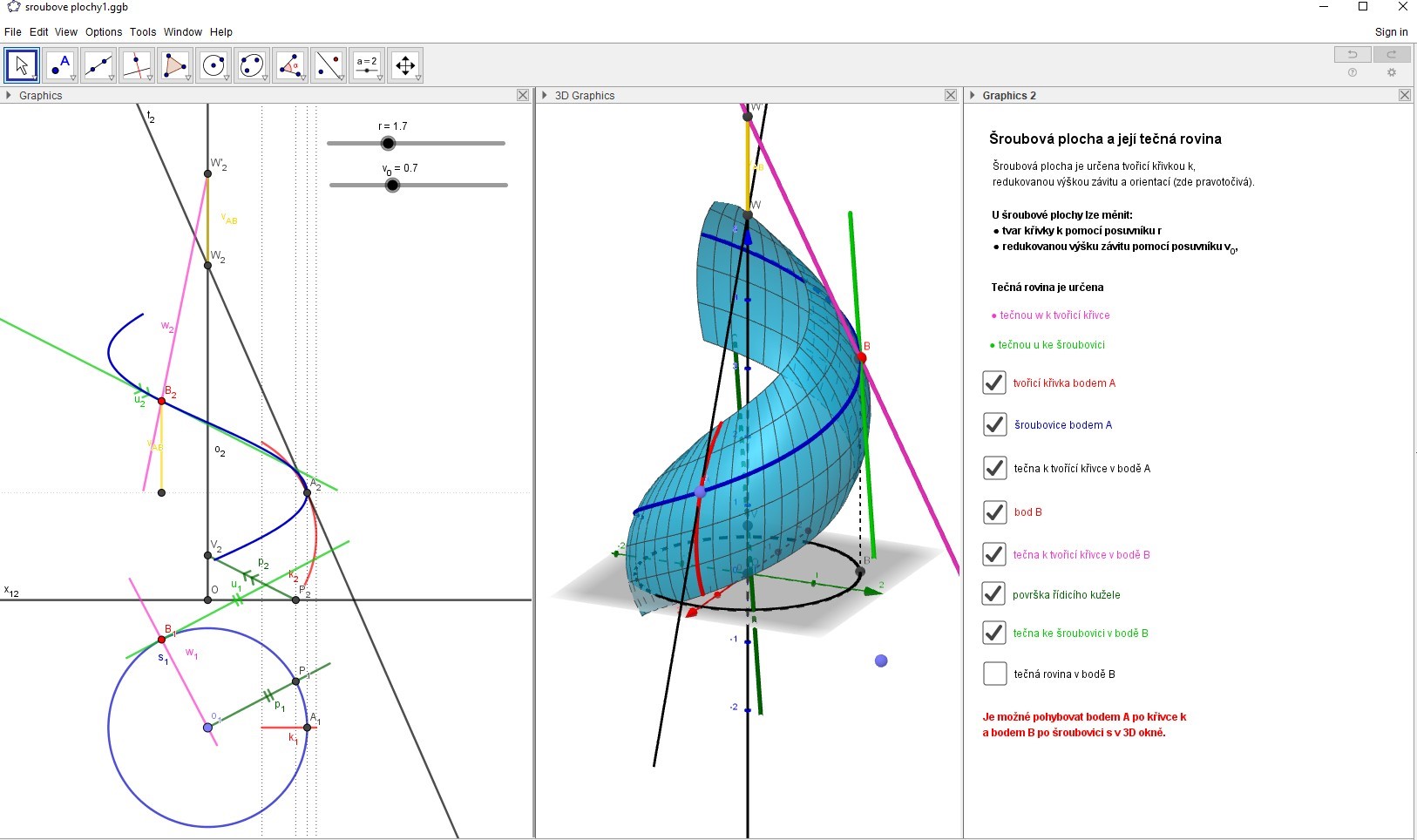
Zde se nejedná o úlohu s konkrétním zadáním (i když by ji tak šlo využít), ale o ilustraci k výkladu problematiky tečné roviny šroubové plochy. Pomocí zaškrtávacích políček je možné zobrazit jen některé prvky jako je tvořící křivka a tečna k ní, šroubovice zadaným bodem a tečna k této šroubovici, popřípadě vizualizovat tečnou rovinu v 3D okně. Opět platí, že změna (např. pohyb bodu v 3D okně) se projeví v obou oknech současně.

Závěrem mohu říct, že práce s GeoGebrou se mi osvědčila, a to i během nouzové distanční výuky na jaře letošního roku, kdy jsem připravila celou sadu řešených příkladů k přednášce. Jedná se o příklady, které při standardní výuce řeším se studenty na tabuli. Zatímco při kontaktní výuce mají studenti možnost se průběžně ptát, přičemž já mohu sledovat, kolik času potřebují na vyřešení zadané úlohy, a podle toho volit tempo výuky, při práci s GeoGebrou tento osobní rozměr samozřejmě bohužel chybí. Studenti však mají alespoň možnost pracovat vlastním tempem, postup při řešení krokovat a dle potřeby se vracet zpět. Ačkoli se nejedná o stoprocentní náhradu standardní výuky, byli studenti s tímto způsobem práce spokojeni a i během zkoušek se ukázalo, že princip úloh, které měli zveřejněné v GeoGebře, zvládli velice dobře.

Aplikaci GeoGebra považuji za velmi praktický nástroj, se kterým lze výborně pracovat nejen v rámci distanční výuky. Se studenty ji rozhodně budeme nadále využívat i při standardní výuce, např. jako další pomoc při domácí přípravě ke zkoušce.

Zaujala vás aplikace GeoGebra a chtěli byste se o ní dozvědět více? Zde naleznete základní informace, návody i materiály vytvořené v GeoGebře ostatními uživateli.

Máte tip na zajímavou aplikaci pro výuku na vysoké škole nebo nápad, jak využít dostupné on-line nástroje, aby byla výuka efektivnější a zajímavější? Podělte se s námi o své zkušenosti. Kontaktujte nás prostřednictvím e-mailu na adrese hokrova@rek.zcu.cz.

Další díly seriálu příkladů dobré praxe on-line výuky na ZČU najdete zde: